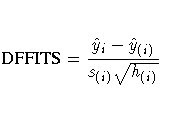Outlier Treatment
A single observation that is substantially different from all other observations can make a large difference in the results of the regression analysis. If a single observation (or small group of observations) substantially changes the results, one would want to know about this and investigate further.
In linear regression, an outlier is an observation with large residual. In other words, it is an observation whose dependent-variable value is unusual given its values on the predictor variables. An outlier may indicate a sample peculiarity or may indicate a data entry error or other problem.
High values are known as upper outliers and low ones are known as lower outliers. Such values should be modified or else they would bias the estimation of the model parameters. The most simple and commonly used outlier treatment technique is by capping the values which are above 99% or below 1% of the population. This means that if a value is above the 99th percentile then it is replaced by the value corresponding to the 99th percentile. Similar capping is done for values below 1st percentile.
Leverage: An observation with an extreme value on a predictor variable is called a point with high leverage. Leverage is a measure of how far an independent variable deviates from its mean. These leverage points can have an effect on the estimate of regression coefficients.
Influence: An observation is said to be influential if removing the observation substantially changes the estimate of coefficients. Influence can be thought of as the product of leverage and outlierness.
Detecting Unusual and Influential Data
o Scatterplots of the dependent variable versus the independent variables
We need to examine the relationship between the dependent variable, Y1, and a continuous predictor, X1. We first look at a scatterplot, with a regression line included to see the relationship between Y and X and decide if it appears to be linear (degree = 1 is used for the regression line). We also look for any outliers. Here is the SAS code:
title "Scatter Plot with Regression Line";
proc sgplot data=a;
reg y=y1 x=x1 / degree=1;
run;
o looking at the largest values of the studentized residuals, leverage, Cook's D, DFFITS and DFBETAs . Here is the code:
proc reg data = best_model ;
model ln_gross_rev =
Tot_unit_AnyProd
Flag_PC
Flag_other
hh_size
online_ordr_amt_avg
age
/ vif collin ;
output out = predicted_output p=Predicted r=Error cookd = CooksD dffits=dffit h=lev;
run;
ods graphics off ;
data a;
set predicted_output ;
cov = finv(0.05,7,518433);
if CooksD > cov then flag_cook = 1;
else flag_cook = 0;
run;
proc freq data = a; tables flag_cook; run;
Ideally, flag_cook = 0 should be 100%. Flag_cook = 1 indicates presence of outliers. Incase of unusual data points, we need to do the proper treatments or remove those data points from the model data (if the percentage of unusual data points are not very high).
Cook's d follows a F dist with (K,n-K) df, where n= number of obs, K=parameters in model(includes intercept)
The lowest value that Cook's D can assume is zero, and the higher the Cook's D is, the more influential the point is. The conventional cut-off point is 4/n. We can either follow the above mentioned method or list any observation above the cut-off point by doing the following. Here is the code for the same:
data xxx(keep = cust_id Tot_unit_AnyProd Flag_PC Flag_other hh_size
online_ordr_amt_avg age_n CooksD); set predicted_output;
where CooksD > (4/518433);
run;
(Note: In this example the model dependent variable was revenue per customer, so the data is at customer level i.e. all the variables are summarized at customer level and one customer is having one row. That is the reason I have kept cust_id variable in the above output. It will help to understand customers are having most influential data point)
Plot the DFFITS statistic by observation number. Observations whose DFFITS’ statistic is greater in magnitude than , where is the number of observations used and is the number of regressors, are deemed to be influential.
DFITS can be either positive or negative, with numbers close to zero corresponding to the points with small or zero influence.
data yyy(keep = cust_id Tot_unit_AnyProd
Flag_PC
Flag_other
hh_size
online_ordr_amt_avg
age dffit) ; set predicted_output;
where abs(dffit)> (2*sqrt(6/518433));
run;
The DFFITS statistic is a scaled measure of the change in the predicted value for the ith observation and is calculated by deleting the ith observation. A large value indicates that the observation is very influential in its neighborhood of the X space.
The above measures are general measures of influence. One can also consider more specific measures of influence that assess how each coefficient is changed by deleting the observation. This measure is called DFBETA and is created for each of the predictors. Apparently this is more computationally intensive than summary statistics such as Cook's D because the more predictors a model has, the more computation it may involve. We can restrict our attention to only those predictors that we are most concerned with and to see how well behaved those predictors are. In SAS, we need to use the ods output OutStatistics statement to produce the DFBETAs for each of the predictors. The names for the new variables created are chosen by SAS automatically and begin with DFB_.
proc reg data = best_model ;
model ln_gross_rev= Tot_unit_AnyProd
Flag_PC Flag_other hh_size online_ordr_amt_avg age_n/influence;
ods Output OutputStatistics= revbetas;
id Cust_cid;
run;
(note: for bigger datasets the html output will be huge, once the code is done no need to save the ods output as all the betas will be stored in the output dataset)
This created six variables, DFB_Tot_unit_AnyProd, DFB_Flag_PC , DFB_Flag_other, DFB_hh_size, DFB_online_ordr_amt_avg and DFB_age
The DFBETAS statistics are the scaled measures of the change in each parameter estimate and are calculated by deleting the ith observation:
where (X'X)jj is the (j,j)th element of (X'X)-1.
In general, large values of DFBETAS indicate observations that are influential in estimating a given parameter. Belsley, Kuh, and Welsch recommend 2 as a general cutoff value to indicate influential observations and (2/sqrt n) as a size-adjusted cutoff.
If a point lies far from the other data in the horizontal direction, it is known as an influential observation. The reason for this distinction is that these points have may have a significant impact on the slope of the regression line. We need to remove influential data points or need to do the proper treatments of influential points.
Now let's look at the leverage's to identify observations that will have potential great influence on regression coefficient estimates. Here is the sample SAS code:
proc univariate data= predicted_output plots plotsize=30;
var lev;
run;
Generally, a point with leverage greater than (2k+2)/n should be carefully examined, where k is the number of predictors and n is the number of observations.
The following table summarizes the general rules of thumb we use for these measures to identify observations worthy of further investigation (where k is the number of predictors and n is the number of observations).
Measure Value
leverage >(2k+2)/n
abs(rstu) > 2
Cook's D > 4/n
abs(DFITS) > 2*sqrt(k/n)
abs(DFBETA) > 2/sqrt(n)
For more details, please refer
http://www.ats.ucla.edu/stat/sas/webbooks/reg/chapter2/sasreg2.htm
Model building
Once the data has been cleaned by missing imputation and outlier treatment, the initial model is built on it. For the initial/ first cut model, all the independent variables are put into the model. The objective is to finally have a limited number of independent variables (5-10) which are significant in all respect, without sacrificing too much on the model performance. The reason behind not-including having too many variables is that the model would be over fitted and would become unstable when tested on the validation sample. The variable reduction is done using forward or backward or stepwise variable selection procedures. These procedures are described below:
Forward Selection - In a forward selection analysis we start out with no predictors in the model. Each of the available predictors is evaluated with respect to how much R2 would be increased by adding it to the model. The one which will most increase R2 will be added if it meets the statistical criterion for entry. With SAS the statistical criterion is the significance level for the increase in the R2 produced by addition of the predictor. If no predictor meets that criterion, the analysis stops. If a predictor is added, then the second step involves re-evaluating all of the available predictors which have not yet been entered into the model. If any satisfy the criterion for entry, the one which most increases R2 is added. This procedure is repeated until there remain no more predictors that are eligible for entry.
Backwards Elimination - In a backwards elimination analysis we start out with all of the predictors in the model. At each step we evaluate the predictors which are in the model and eliminate any that meet the criterion for removal.
Stepwise Selection - With fully stepwise selection we start out just as in forwards selection, but at each step variables that are already in the model are first evaluated for removal, and if any are eligible for removal, the one whose removal would least lower R2 is removed. You might wonder why a variable would enter at one point and leave later -- well, a variable might enter early, being well correlated with the criterion variable, but later become redundant with predictors that follow it into the model.
An entry significance level of 0.15, specified in the slentry=0.15 option, means a variable must have a p-value < 0.15 in order to enter the model during forward selection and stepwise regression. An exit significance level of 0.05, specified in the slstay=0.05 option, means a variable must have a p-value > 0.05 in order to leave the model during backward selection and stepwise regression. One can change the entry and exit criteria based on the situation and requirement.
The following SAS code performs the forward selection method by specifying the option selection=forward.
proc reg data=a outest=est1;
model y=x1 x2 x3 x4 x5 x6 x7 x8 x9 x10…..Xn / slstay=0.15 slentry=0.15
selection=forward ss2 sse aic;
output out=out1 p=p r=r; run;
The following SAS code performs the backward elimination method by specifying the option selection=backward.
proc reg data=a outest=est2;
model y=x1 x2 x3 x4 x5 x6 x7 x8 x9 x10….Xn / slstay=0.05 slentry=0.15
selection=backward ss2 sse aic;
output out=out1 p=p r=r; run;
The following SAS code performs stepwise regression by specifying the option selection=stepwise.
proc reg data=a outest=est3;
model y=x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 …Xn/ slstay=0.05 slentry=0.15
selection=stepwise ss2 sse aic;
output out=out3 p=p r=r; run;
Once the first cut model is ready, one might have to couple of manual iteration based on business logic. Once the first cut model is ready, one needs to check the multicollinearity. One can use the following code for the same:
proc reg data=a outest=parameter;
model y=x1 x2 x3 x4 x5 x6 x7 x8 x9 x10…..xn /
/ vif collin;
output out=out3 p=p r=r;
run;
Thursday, August 12, 2010
Saturday, August 7, 2010
My Understanding about Linear Regression - Part II
Important terminologies
Variables: Variables are measurements of occurrences of a recurring event taken at regular intervals or measurements of different instances of similar events that can take on different possible values. E.g. the price of gasoline recorded at monthly intervals, the height of children between the age of 6 and 10, Revenue per customer.
Dependent Variable: A variable whose value depends on the value of other variables in a model. E.g. revenue from customer, which is directly dependent on their purchase quantity and price of the product/s.
Independent Variables: Variables whose value is not dependent on other variables in a model. E.g. in the above example, the price of corn would be one of the independent variables driving the price of corn oil. An independent variable is specific to a model and a variable that is independent in one model can be dependent in another.
Lurking Variables: If non-linear trends are visible in the relationship between an explanatory and dependent variable, there may be other influential variables to consider. A lurking variable exists when the relationship between two variables is significantly affected by the presence of a third variable which has not been included in the modeling effort. Since such a variable might be a factor of time (for example, the effect of political or economic cycles), a time series plot of the data is often a useful tool in identifying the presence of lurking variables.
Residual: Once a regression model has been fit to a group of data, examination of the residuals (the deviations from the fitted line to the observed values) allows the modeler to investigate the validity of his or her assumption that a linear relationship exists. Plotting the residuals on the y-axis against the explanatory variable on the x-axis reveals any possible non-linear relationship among the variables, or might alert the modeler to investigate lurking variables.
Extrapolation: Whenever a linear regression model is fit to a group of data, the range of the data should be carefully observed. Attempting to use a regression equation to predict values outside of this range is often inappropriate, and may yield incredible answers. This practice is known as extrapolation. Consider, for example, a linear model which relates weight gain to age for young children. Applying such a model to adults, or even teenagers, would be absurd, since the relationship between age and weight gain is not consistent for all age groups.
Modeling and Validation Population
Once the dependent variable has been defined, the entire population is split into modeling and validation population. This split is done in a random way, so that the average value of dependent variable for both these samples is roughly the same. It is assumed that the characteristics of the independent variables would be similar in the two samples, as it is a random split. The modeling population is used to build the model and then it is implemented on the validation population. The performance of a model should be similar in both modeling and validation samples.
Here is the sample SAS code:
data wl_model(drop=x) wl_validation(drop=x);
set vintage24_48_all_cust_1;
x=ranuni(2345);if x < 0.5 then output wl_model;
else output wl_validation;run;
proc means data = vintage24_48_all_cust_1 mean; var ln_gross_rev;
run;
proc means data = wl_model mean; var ln_gross_rev; run;
proc means data = wl_validation mean; var ln_gross_rev; run;
Instead of 50:50 split, one can use 60:40 or 70:30 split for Modeling and validation dataset.
Missing Imputation and normality of dependent variable
All the independent variables and the dependent variable that go into the model should not have any missing values. If the dependent variable has a missing value for an observation, which is rarely the case, then it should be discarded. For Linear regression, if the dependent variable is skewed, one can use the log transformation of the dependent variable so that the dependent variable is normally distributed. Here is the code to perform log transformation:
data dep_var_1;
set dep_var;
ln_gross_rev =log(gross_rev);
run;
One can use proc univariate to plot the dependent variable. The following code can be used:
proc univariate data= dep_var_1;
var ln_gross_rev;
histogram / normal
midpoints = 1 2 3 4 5 6 7 8 9 10
ctext = blue;
run;
For the independent variables, the missing values are replaced / imputed. Some of the commonly used imputation techniques include :
1. Replacing by median,
2. Replaced by mode,
3. Replaced by 0
4. Replaced by any other logical values.
Median is preferred to mean because it is not impacted by extreme values. Mode is used when the variable is discrete or categorical, where the mode is the most frequently occurring value. 0 is mostly used for indicator/dummy/binary variables. Other logical values can also be used based on their business implications.
Variables: Variables are measurements of occurrences of a recurring event taken at regular intervals or measurements of different instances of similar events that can take on different possible values. E.g. the price of gasoline recorded at monthly intervals, the height of children between the age of 6 and 10, Revenue per customer.
Dependent Variable: A variable whose value depends on the value of other variables in a model. E.g. revenue from customer, which is directly dependent on their purchase quantity and price of the product/s.
Independent Variables: Variables whose value is not dependent on other variables in a model. E.g. in the above example, the price of corn would be one of the independent variables driving the price of corn oil. An independent variable is specific to a model and a variable that is independent in one model can be dependent in another.
Lurking Variables: If non-linear trends are visible in the relationship between an explanatory and dependent variable, there may be other influential variables to consider. A lurking variable exists when the relationship between two variables is significantly affected by the presence of a third variable which has not been included in the modeling effort. Since such a variable might be a factor of time (for example, the effect of political or economic cycles), a time series plot of the data is often a useful tool in identifying the presence of lurking variables.
Residual: Once a regression model has been fit to a group of data, examination of the residuals (the deviations from the fitted line to the observed values) allows the modeler to investigate the validity of his or her assumption that a linear relationship exists. Plotting the residuals on the y-axis against the explanatory variable on the x-axis reveals any possible non-linear relationship among the variables, or might alert the modeler to investigate lurking variables.
Extrapolation: Whenever a linear regression model is fit to a group of data, the range of the data should be carefully observed. Attempting to use a regression equation to predict values outside of this range is often inappropriate, and may yield incredible answers. This practice is known as extrapolation. Consider, for example, a linear model which relates weight gain to age for young children. Applying such a model to adults, or even teenagers, would be absurd, since the relationship between age and weight gain is not consistent for all age groups.
Modeling and Validation Population
Once the dependent variable has been defined, the entire population is split into modeling and validation population. This split is done in a random way, so that the average value of dependent variable for both these samples is roughly the same. It is assumed that the characteristics of the independent variables would be similar in the two samples, as it is a random split. The modeling population is used to build the model and then it is implemented on the validation population. The performance of a model should be similar in both modeling and validation samples.
Here is the sample SAS code:
data wl_model(drop=x) wl_validation(drop=x);
set vintage24_48_all_cust_1;
x=ranuni(2345);if x < 0.5 then output wl_model;
else output wl_validation;run;
proc means data = vintage24_48_all_cust_1 mean; var ln_gross_rev;
run;
proc means data = wl_model mean; var ln_gross_rev; run;
proc means data = wl_validation mean; var ln_gross_rev; run;
Instead of 50:50 split, one can use 60:40 or 70:30 split for Modeling and validation dataset.
Missing Imputation and normality of dependent variable
All the independent variables and the dependent variable that go into the model should not have any missing values. If the dependent variable has a missing value for an observation, which is rarely the case, then it should be discarded. For Linear regression, if the dependent variable is skewed, one can use the log transformation of the dependent variable so that the dependent variable is normally distributed. Here is the code to perform log transformation:
data dep_var_1;
set dep_var;
ln_gross_rev =log(gross_rev);
run;
One can use proc univariate to plot the dependent variable. The following code can be used:
proc univariate data= dep_var_1;
var ln_gross_rev;
histogram / normal
midpoints = 1 2 3 4 5 6 7 8 9 10
ctext = blue;
run;
For the independent variables, the missing values are replaced / imputed. Some of the commonly used imputation techniques include :
1. Replacing by median,
2. Replaced by mode,
3. Replaced by 0
4. Replaced by any other logical values.
Median is preferred to mean because it is not impacted by extreme values. Mode is used when the variable is discrete or categorical, where the mode is the most frequently occurring value. 0 is mostly used for indicator/dummy/binary variables. Other logical values can also be used based on their business implications.
OPTIONS ON THE PROC SQL STATEMENT
Restricting Row Processing with the INOBS= and OUTOBS= Options
There are several useful options that can be used in the PROC SQL statement to help control the appearance of the report. Note that once coded, these options will apply to all SELECT statements within the PROC SQL step unless a RESET statement is used:
PROC SQL INOBS=5 OUTOBS=4 DOUBLE;
SELECT STORE_NAME, (GROSS_SALES * .05) AS TAX
FROM Online_Sales;
QUIT;
INOBS=n
Restricts the number of rows (observations) that PROC SQL retrieves from any single source. This is very useful for debugging queries on large table.
For example, if you specify INOBS=10, then PROC SQL uses only 10 rows from any table or view that is specified in a FROM clause. If you specify INOBS=10 and join two tables without using a WHERE clause, then the resulting table (Cartesian product) contains a maximum of 100 rows. The INOBS= option is similar to the SAS system option OBS=.
OUTOBS=n
Restricts the number of rows (observations) in the output. For example, if you specify OUTOBS=10 and insert values into a table by using a query, then PROC SQL inserts a maximum of 10 rows into the resulting table. Please refer output #1.
For example, we have one dataset called ONLINE_SALES:
output #1
The CALCULATED component refers to a previously calculated variable so recalculation is not necessary. The CALCULATED component must refer to a variable created within the same SELECT statement. Please refer output #2.
PROC SQL ;
SELECT STORE_NAME, (GROSS_SALES * .05) AS TAX,
CALCULATED TAX * .01 AS REBATE
FROM Online_Sales;
QUIT;
Output #2
There are several useful options that can be used in the PROC SQL statement to help control the appearance of the report. Note that once coded, these options will apply to all SELECT statements within the PROC SQL step unless a RESET statement is used:
PROC SQL INOBS=5 OUTOBS=4 DOUBLE;
SELECT STORE_NAME, (GROSS_SALES * .05) AS TAX
FROM Online_Sales;
QUIT;
INOBS=n
Restricts the number of rows (observations) that PROC SQL retrieves from any single source. This is very useful for debugging queries on large table.
For example, if you specify INOBS=10, then PROC SQL uses only 10 rows from any table or view that is specified in a FROM clause. If you specify INOBS=10 and join two tables without using a WHERE clause, then the resulting table (Cartesian product) contains a maximum of 100 rows. The INOBS= option is similar to the SAS system option OBS=.
OUTOBS=n
Restricts the number of rows (observations) in the output. For example, if you specify OUTOBS=10 and insert values into a table by using a query, then PROC SQL inserts a maximum of 10 rows into the resulting table. Please refer output #1.
For example, we have one dataset called ONLINE_SALES:
output #1
THE CALCULATED OPTION
The CALCULATED component refers to a previously calculated variable so recalculation is not necessary. The CALCULATED component must refer to a variable created within the same SELECT statement. Please refer output #2.
PROC SQL ;
SELECT STORE_NAME, (GROSS_SALES * .05) AS TAX,
CALCULATED TAX * .01 AS REBATE
FROM Online_Sales;
QUIT;
Output #2
Thursday, August 5, 2010
Use of LIKE in proc sql
Look at the Customer Table, and say you wanted to see all people whose last names started with "m"; The syntax would be:
data customer;
input Cust_F_name $5. Cust_L_Name $4. id;
cards;
anjo bana 201
minu mana 211
sinu shan 444
sinu malu 442
;run;
proc sql;
SELECT id, Cust_F_name
FROM customer
WHERE Cust_L_Name LIKE 'm%';
quit;
The percent sign (%) is used to represent any possible character (number, letter, or punctuation) or set of characters that might appear after the "m". To find those people with LastName's ending in "m", use '%m', or if you wanted the "m" in the middle of the word, try '%m%'. The '%' can be used for any characters in the same position relative to the given characters. NOT LIKE displays rows not fitting the given description.
data customer;
input Cust_F_name $5. Cust_L_Name $4. id;
cards;
anjo bana 201
minu mana 211
sinu shan 444
sinu malu 442
;run;
proc sql;
SELECT id, Cust_F_name
FROM customer
WHERE Cust_L_Name LIKE 'm%';
quit;
The percent sign (%) is used to represent any possible character (number, letter, or punctuation) or set of characters that might appear after the "m". To find those people with LastName's ending in "m", use '%m', or if you wanted the "m" in the middle of the word, try '%m%'. The '%' can be used for any characters in the same position relative to the given characters. NOT LIKE displays rows not fitting the given description.
Tuesday, August 3, 2010
My Understanding about Linear Regression - Part I
What is linear regression?
Linear regression attempts to model the relationship between two variables by fitting a linear equation to observed data. One variable is considered to be an explanatory variable, and the other is considered to be a dependent variable. Two-variable linear regression model is a model in which the dependent variable is expressed as a linear function of only a single explanatory variable. The most common method for fitting a regression line is the method of least-squares. This method calculates the best-fitting line for the observed data by minimizing the sum of the squares of the vertical deviations from each data point to the line (if one point lies on the fitted line exactly, then its vertical deviation is 0).
Multivariate linear regression
Multivariate regression takes into account several predictive variables simultaneously.
The model is now expressed as
yi = b 0 + b 1 x 1i + b 1 x 2i + … b n x ni
Where n = the number of independent variables
yi = expected or predicted value of the dependent variable for case i
b 0 = the intercept (if all x’s are zero, the expected value of y is b 0 )
b j = the slope (for every one unit increase in xj , y is expected to change by b j units, given that the other independent variables are held constant)
x i = the value of the independent variable for case i
Assumptions of Linear Regression
1. Homoscedasticity – the variance of the error terms is constant for each value of x.
2. Linearity – the relationship between each x and y is linear. To check this, look at the plot(s) of the residuals versus the X value(s). You don’t want to see a clustering of positive residuals or a clustering of negative residuals.
3. Normally Distributed Error Terms – the error terms follow the normal distribution.
4. Independence of Error Terms – successive residuals are not correlated, if they are correlated, it is known as autocorrelation. If possible, use the Durbin Watson statistic to check this.
Frequently used forms of Linear Regression
(i) Log linear Model
Log linear model is useful in case we need to measure the elasticity
lnY=β0+ β 1(lnX1)+ β2(lnx2) + ……….+ βn(lnxn) + Error.
Here, β 1 gives the elasticity of Y with respect to X, i.e., the percentage change in Y with respect to percentage change in X. This equation is also known as the constant elasticity form as in this equation, the elasticity of y with respect to changes in x as δ lny/δ lnxn = βn, which does not vary with xn . This loglinear form is often used in models of demands and production.
(ii) Semilog Model
ln(Y)= β0+ β 1X + Error.
Here, β 1 gives the relative change in Y for a absolute change in the value of X.
A semilog model is often used to model growth rates
Derivation: Yt = Y0 (1+r)^t, which is the compound interest formula.
Taking log , log(Yt)=log(Y0)+tlog(1+r) = β0+ β1 (X).
β1 = relative change in regressand/absolute change in regressor
If we multiply the relative change in Y by 100, will then give the percentage change, or the growth rate, in Y for an absolute change in X, the regressor. That is, 100 times β1 gives the growth rate in Y; is
Another type of semi log model
Y= β0+ β 1 (lnX)+Error.
Unlike the growth model, in which we are interested in finding the percent growth in Y for an absolute change in X, here we want to find the absolute change in Y for a percent change in X.
β1 = change in Y/change in ln X
= change in Y/relative change in X
Linear regression attempts to model the relationship between two variables by fitting a linear equation to observed data. One variable is considered to be an explanatory variable, and the other is considered to be a dependent variable. Two-variable linear regression model is a model in which the dependent variable is expressed as a linear function of only a single explanatory variable. The most common method for fitting a regression line is the method of least-squares. This method calculates the best-fitting line for the observed data by minimizing the sum of the squares of the vertical deviations from each data point to the line (if one point lies on the fitted line exactly, then its vertical deviation is 0).
Multivariate linear regression
Multivariate regression takes into account several predictive variables simultaneously.
The model is now expressed as
yi = b 0 + b 1 x 1i + b 1 x 2i + … b n x ni
Where n = the number of independent variables
yi = expected or predicted value of the dependent variable for case i
b 0 = the intercept (if all x’s are zero, the expected value of y is b 0 )
b j = the slope (for every one unit increase in xj , y is expected to change by b j units, given that the other independent variables are held constant)
x i = the value of the independent variable for case i
Assumptions of Linear Regression
1. Homoscedasticity – the variance of the error terms is constant for each value of x.
2. Linearity – the relationship between each x and y is linear. To check this, look at the plot(s) of the residuals versus the X value(s). You don’t want to see a clustering of positive residuals or a clustering of negative residuals.
3. Normally Distributed Error Terms – the error terms follow the normal distribution.
4. Independence of Error Terms – successive residuals are not correlated, if they are correlated, it is known as autocorrelation. If possible, use the Durbin Watson statistic to check this.
Frequently used forms of Linear Regression
(i) Log linear Model
Log linear model is useful in case we need to measure the elasticity
lnY=β0+ β 1(lnX1)+ β2(lnx2) + ……….+ βn(lnxn) + Error.
Here, β 1 gives the elasticity of Y with respect to X, i.e., the percentage change in Y with respect to percentage change in X. This equation is also known as the constant elasticity form as in this equation, the elasticity of y with respect to changes in x as δ lny/δ lnxn = βn, which does not vary with xn . This loglinear form is often used in models of demands and production.
(ii) Semilog Model
ln(Y)= β0+ β 1X + Error.
Here, β 1 gives the relative change in Y for a absolute change in the value of X.
A semilog model is often used to model growth rates
Derivation: Yt = Y0 (1+r)^t, which is the compound interest formula.
Taking log , log(Yt)=log(Y0)+tlog(1+r) = β0+ β1 (X).
β1 = relative change in regressand/absolute change in regressor
If we multiply the relative change in Y by 100, will then give the percentage change, or the growth rate, in Y for an absolute change in X, the regressor. That is, 100 times β1 gives the growth rate in Y; is
Another type of semi log model
Y= β0+ β 1 (lnX)+Error.
Unlike the growth model, in which we are interested in finding the percent growth in Y for an absolute change in X, here we want to find the absolute change in Y for a percent change in X.
β1 = change in Y/change in ln X
= change in Y/relative change in X
Feedback option in Proc sql
The FEEDBACK option expands a SELECT * (ALL) statement into the list of columns that the statement represents.
The FEEDBACK option also displays the resolved values of macros and macro variables.
For example, the following query is expanded in the SAS log:
PROC SQL feedback; CREATE TABLE vintage24_48_all_tran AS SELECT b.HH_id, a.* FROM online_base_data AS a INNER JOIN demographic AS b ON (b.cust_no = a.cust_id)
ORDER BY a.cust_id; QUIT;
Expanded SELECT * Statement
NOTE: Statement transforms to:
select B.HH_id, A. cust_id, A.product_no, A.serial_no,
A.purch_dt, A.order_no, A.discount_amt, A._unit_price, A.tax_amt,
A.channel, A.coupon, A.payment_amt, A.Last_dt_anyProd, A.First_dt_anyProd, A.customer, A.gross_value_cust
from work.online_base_data A inner join WORK.demographic B on B. cust_no = A.cust_id
order by A.cust_id asc;
The FEEDBACK option also displays the resolved values of macros and macro variables.
For example, the following query is expanded in the SAS log:
PROC SQL feedback; CREATE TABLE vintage24_48_all_tran AS SELECT b.HH_id, a.* FROM online_base_data AS a INNER JOIN demographic AS b ON (b.cust_no = a.cust_id)
ORDER BY a.cust_id; QUIT;
Expanded SELECT * Statement
NOTE: Statement transforms to:
select B.HH_id, A. cust_id, A.product_no, A.serial_no,
A.purch_dt, A.order_no, A.discount_amt, A._unit_price, A.tax_amt,
A.channel, A.coupon, A.payment_amt, A.Last_dt_anyProd, A.First_dt_anyProd, A.customer, A.gross_value_cust
from work.online_base_data A inner join WORK.demographic B on B. cust_no = A.cust_id
order by A.cust_id asc;
Subscribe to:
Posts (Atom)